 たくみ刑事
たくみ刑事中学で習う数学の「図形の証明」って社会人になって何の役に立つの?
犯罪捜査に「図形の証明」が役立つってホント?
図形の証明と、犯罪捜査は、意外な共通点があります。刑事がやる犯罪捜査は、考えの組み立て方が『図形の証明』に似ているんです。
犯罪捜査の現場では、証明の考え方が、いろんな条件から結論を導き出すために、どのピースが必要かを思考するのに大いに役立っています。
まずは、『図形の証明って、数学のどんな問題だったっけ?』と言うあなたの為に、図形の証明について簡単に復習しておきましょう。分かっている方は、目次から飛ばしてください。
数学で習った『図形の証明』って、どんなだっけ?


図形の証明とは
図形の証明とは、
- 数学的事実(定理や命題)が正しいという理由を論理的に主張し、説明する文章のこと
なんか難しい?ので、どんなものだったのか問題をみて、思い出してみましょう。
2つの三角形が合同であるという証明とは
★【問題】★
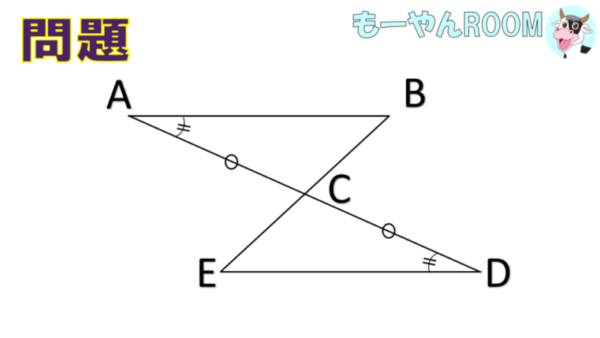
AC=DC、
∠BAC=∠EDCのとき、
△ABC≡△DECであることを証明せよ。



- あ~っっ無理無理無理!って思った人!
ちょっと待って! - わかりやすく説明しますね。
この問題は、
- AC=DC
(辺ACと辺DCは同じ長さ:図の「〇」印の辺) - ∠BAC=∠EDC
(角BACと角EDCは同じ角度:図の「||」印の角度)
という2つの仮定・条件に基づき、
- △ABC≡△DEC
(三角形ABCと三角形DECは合同:「≡」は合同の記号)
2つの三角形が合同であることを証明せよ。という問題です。
まずここで、
- 合同とは
- 三角形の合同条件
について思い出しておきましょう。
合同とは
2つの図形が、ぴったり重なり合うこと。
つまり、向きは違うけど、まったく同じ形で同じ大きさということ。
三角形の合同条件とは
- ① 3組の辺がそれぞれ等しい
- ② 2組の辺とその間の角がそれぞれ等しい
- ③ 1組の辺とその両端の辺がそれぞれ等しい
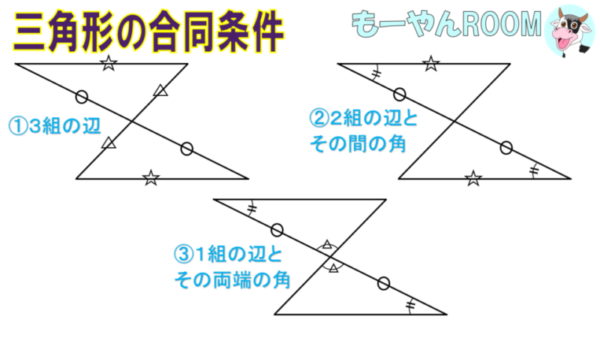

この3つの条件うち、1つでも証明できれば、二つの三角形は合同であると証明される。
★【問題】★に戻ります。


- AC=DC
- ∠BAC=∠EDC
という2つの仮定・条件があります。



3つの三角形の合同条件のうち
「2組の辺とその間の角がそれぞれ等しい」
「1組の辺とその両端の辺がそれぞれ等しい」
のどちらかを証明すれば良さそうだね。
もうお分かりと思いますが、
- ∠ACBと∠DCEは、「対頂角」なので、等しい
ですよね。
対頂角とは、2つの直線が交わるときに向かい合う角のことです。
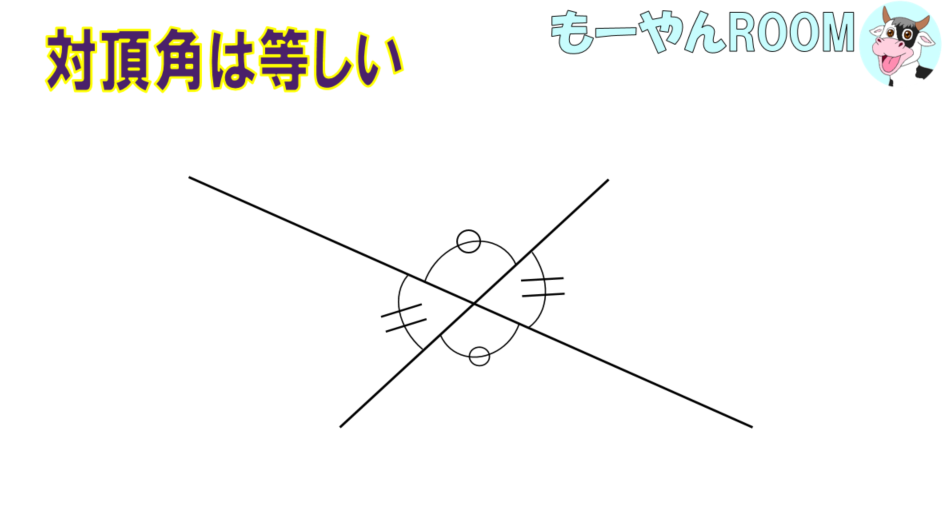

これも
- 「見た感じ等しい」ではダメで
- 「対頂角だから等しい」と言わなければ証明になりません。
∴(ゆえに)
- 1組の辺とその両端の辺がそれぞれ等しい
から、2つの三角形は合同であると証明できる訳です。
数学的な解答は、この様になります。
★【数学的な解答】★
△ABCと△DECおいて、
仮定より、AC=DC、∠BAC=∠EDC
対頂角は等しいので、∠ACBと∠DCE
∴(ゆえに)1組の辺とその両端の角がそれぞれ等しいので
△ABC≡△DEC
基礎的な図形の証明でしたが、ちょっと思い出していただけましたでしょうか?
中学生の時は、もちろんもっと複雑な図形の証明を勉強していたと思います。
刑事の犯罪捜査に、図形の証明がどう役立つのか


犯罪捜査で必要な証拠とは
犯罪の証明というのは、犯罪事実(A男がその犯罪を犯したという事実)が正しいという理由を客観的事実に基づいて主張し、説明することです。
ちょっと分かりにくいので、具体例で説明しますね。
犯罪捜査ではどんな証明をしているか
空き巣事件の捜査って、実際にはどんな捜査をするのでしょうか?
犯人がAという男であるということを証明しなければ、A男の逮捕状を請求することができません。
証拠を見つけ出し、犯罪を証明するという過程は、図形の証明と同じです。


空き巣事件の犯罪の証明とは
空き巣事件を例に、実際の捜査で、どんな証拠を集めるか見てみましょう。
被害に遭っていた事実の特定
- 〇月〇日〇時頃に、被害者B宅で、窓ガラスが割られて侵入され、現金が盗まれたという証拠
- タンスの引き出しに現金が入っていたという証拠
A男が犯人である証明
- タンスの引き出しにA男の指紋が付いていた証拠
- A男が、被害者B宅に入る可能性が、窃盗目的以外では考えられないという証拠
- A男が、被害日時のアリバイがないという証拠
(※ 実際には、もっとたくさんの証拠を集めます)
このような集めた証拠を、『逮捕状請求書』という書類に証拠を記載して、裁判所に逮捕状を請求します。
逮捕状請求書によって、裁判官に対して『犯罪の証明』(A男が空き巣事件の犯人であるという証明)をして、逮捕状が発付されるんです。



犯罪の証明が不十分だと判断されて、逮捕状が出ないこともある。
厳正な令状審査を受けるんだ。
証拠を積み重ねることで、犯人がA男であることを「証明」する訳だ!
数学風に書くと
∴(ゆえに)空き巣事件の犯人はA男



本当だ!
「図形の証明」と「犯罪の証明」は似ていますね。
盗犯刑事の魅力・やりがいについては、こちらで解説しました。
≫盗犯刑事4つの魅力と3つの苦労
刑事の魅力・やりがいは、こちらをご覧ください。
≫刑事の魅力・やりがい!刑事になりたいあなたへ
中学2年で証明を学ぶ理由


厚生労働省が示す学習指導要領
厚生労働省が示す中学校学習指導要領によると、証明の意味については
数学的な推論を行う前に命題の「仮定」と「結論」をはっきりさせ・・・「仮定」から「結論」を導くこと,それが証明である
思考力・判断力・表現力を身に着けるために、
第2学年では,三角形・・などの・・性質を,数学的な推論を用いて調べ・・・図形をよく観察したり・・その推論の過程を他者に伝わるように分かりやすく表現できるようにする。
と書かれています。
中学2年生で、基本的な平面図形の性質を見いだし、平行線や角の性質をもとにしてそれらを確かめ、説明すること(証明すること)によって、思考力・判断力・表現力を身に着けることが、図形の証明を中学で勉強する理由のようです。
※厚生労働省 学習指導要領はコチラ
なぜ証明を習う必要があるのか?
見た感じ、正しいと思えることでも、論理的に証明ができなければ、実は間違っている可能性があります。
証明は、自らの主張が正しいということを保証して、人に説明・説得をする手段と言えます。
こういった思考力・判断力・表現力を身につけるために、図形を題材にして学ぶということかも知れません。
証明が 社会人として役立つのか


一軒の家があります。
見た感じでは、頑丈な造りで、多少の地震が来ても大丈夫そうです。
また、過去に震度7の地震が起きた時も、大丈夫でした。
この家について『再度、震度7の地震があっても大丈夫だ』という仮定は、正しいと言えるでしょうか?
答えはNOです。



建築士などが論理的に証明しなければ「また震度7の地震があっても大丈夫」と保証・証明することはできません。
このように、思考力・判断力・表現力・専門的知識を身に着けて、自らの主張が正しいことを保証し、人に説明・説得をするために、中学で『証明』を学ぶのです。
そして、中学で学んだ図形の証明が、社会人として活躍するための基礎学習となっているのです。
まとめ
★数学で習った『図形の証明』って、どんなだっけ?
- 図形の証明とは
- 2つの三角形が合同であるという証明とは
★刑事の犯罪捜査に、図形の証明がどう役立つのか
- 犯罪捜査で必要な証拠とは
- 犯罪捜査ではどんな証明をしているか
- 空き巣事件の犯罪の証明とは
★中学2年で証明を学ぶ理由
- 厚生労働省が示す学習指導要領
- なぜ証明を習う必要があるのか?
- 証明が 社会人として役立つのか
おまけ 『犯罪捜査はチームプレー』



図形の証明が、犯罪捜査に欠かせないことはわかりました。
僕は「図形の証明」が苦手だから、刑事には向いていないかも。
そんなことはありません。
刑事は、それぞれ色々な得意が集まって出来ているチームです。
- 取り調べが得意
- 聞き込みが得意
- 図面など資料作成が得意
- データ分析が得意
- ひらめきが優れている
- 組み立てが優れている
- 一つの事をやり続ける根気が優れている
など、挙げればキリがないほどたくさんの得意で成り立っています。



たくみ刑事は、データ分析が得意だろ?
それを伸ばしてチームに貢献するといいよ。



チームでひとつの事件をやり遂げるんですね。
『チームプレー』の考え方は、もーやんが駆け出しの刑事の頃、警視庁のベテラン女性先輩刑事から教わったことです。
20年以上前の言葉を、今でも大切にしています。



最後まで読んでくれてありがとうございます!
ご感想、ご質問をLINE無料相談へ書き込んでもらえると嬉しいです。










